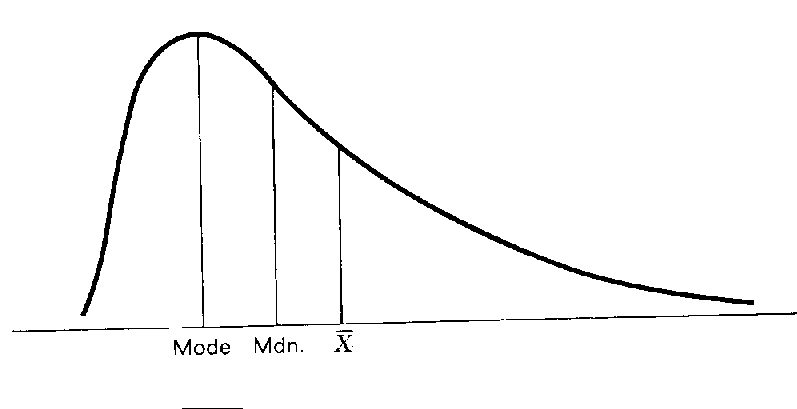
DIAGRAM WHEN THE DATA IS SKEWED, THE 3 MEASURES CANNOT COINCIDE
Z SCORES Data with different values are better compared by converting to a common measure. The common measure used is the distance from the mean in terms of standard deviation. This is done by way of "Z" scores. Each value is converted to standard deviations with the following formula: Z = (X-AVG)/STD Where: X = the data to be converted AVG = mean for the data group STD = standard deviation for the data group The Z scores for the Summerton data are: TABLE DATA Z SCORES 250 -1.071 300 -0.913 350 -0.755 350 -0.755 400 -0.597 400 -0.597 400 -0.597 450 -0.440 450 -0.440 450 -0.440 500 -0.282 500 -0.282 600 0.033 650 0.191 700 0.349 750 0.507 1000 1.295 1200 1.926 1500 2.873 Z scores can be used to directly compare two sets of data even though there may be differences
in magnitude between the two. They will be used to transform raw data in subsequent statistical
