law of diminishing returns

LAW OF DIMINISHING RETURNS

The law of diminishing returns is also known as the law of variable proportions. It is of particular importance in real estate development. The law states:

When the quantity of 1 production input is increased by equal increments (with the quantities of another production input remaining fixed) the resulting output of product will, at some point, begin to decrease.

EXAMPLE

If the height of building is the variable input and land area the fixed input, as the building becomes taller, a point is eventually reached where the net rental income will decline. This is not because of a decrease in gross rental income which will probably increase with better views, naming rights etc, but because the cost of construction and operating costs increase at a greater rate with height. That is, the marginal net annual income falls to point below the marginal cost of operation and construction. The concept is shown in the table below:

TABLE

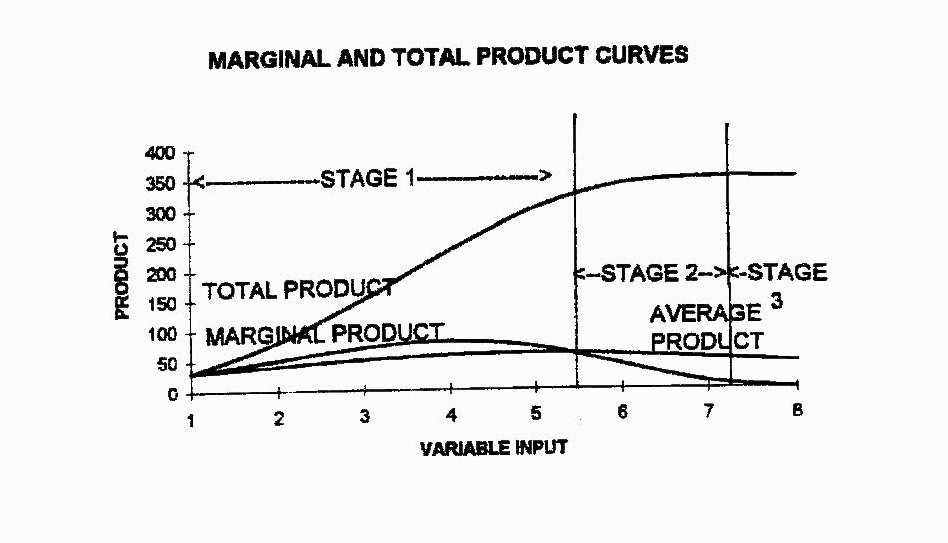
DIMINISHING MARGINAL PRODUCT
HEIGHT (FLOORS)	TOTAL NET INCOME	AVERAGE PRODUCT	MARGINAL PRODUCT
1	30 000	30 000	30 000
2	80 000	40 000	50 000
3	150 000	50 000	70 000
4	230 000	57 500	80 000
5	300 000	60 000	70 000
6	340 000	56 666	40 000
7	350 000	50 000	10 000
8	350 000	43 750	0

The average product is the average output per unit of variable input; the number of floors. The marginal product is the marginal or added product resulting from employing 1 additional unit of the variable input.

The marginal product is important because a profit maximizing developer must compare the cost of adding a marginal unit with the expected marginal return (in this case the present value of net rent) of the additional unit. This is illustrated as a general graph in the diagram below:

MARGINAL & TOTAL PRODUCT CURVES

The diagram below illustrates the effect of the rule on the height of buildings in the CBD. As accessibility falls away from the CBD centre the height of buildings fall.

SYDNEY CBD SKYLINE

The marginal product curve always cuts the average product curve from above at its highest point (maximum average product). This must be true because the addition of a unit of productive input that produces a marginal product less than the previous average must always lower the average. Total product always reaches maximum point at the same input at which marginal product reaches zero. A negative marginal product reduces the total output. Production will always be in stage 2 and the company should not produce in stage 3 because total output would be reduced with each additional unit of the variable input.

In stage 1, output per unit of variable input is not maximised. The producer can increase average output per unit of variable input by simply increasing the units of the variable input. Even if fixed inputs were free, the profit maximising producer would extend output into stage 2 as long as the marginal revenue per unit is greater than the per unit cost of the variable input. To determine exactly where within stage 2 a profit maximising producer should operate, it is necessary to know the relative cost of the fixed and variable services.