depth formulae

The older style of shopping centres in the major cities of Australia typically, have the following "strip" or “ribbon” layout:

RIBBON OR STRIP SHOPPING CENTRE

Such centres are also known as ribbon or linear shopping centres and are characterized by busy arterial roads with shops fronting the street. Lock up shops are typical in such centres and value depends largely on passing pedestrian and vehicular traffic. Generally, the greater the passing traffic, the greater the value of the shop.

SHOP FRONT

The shopfront is most important as it serves the shop for:

Therefore, land at the shopfront is more valuable than the rear land. From this simple assumption a number of depth formulae have been developed as models for the valuation of rear land relative to front land.

Depth formulae are quantitative methods for the estimation of land value at different depths, mainly American, and have been developed for the mass appraisal of large cities such as Chicago and New York. The method has also been approved for the assessment of compensation payable after a compulsory acquisition. For example, in Selbourne Chambers v VG (1982), 30 The Valuer 430 where the 4 3 2 1 rule was adopted.

The valuer must remember that depth formulae are only as good as the sales upon which they are based and he/she must be able to prove the valuation with comparable sales. Where a number of commercial land values have to be determined for example, for rating and taxing purposes, the valuer should construct a graph of the sales to find a common curve so that other values can be interpolated from the sale evidence.

If the graph has been constructed from comparable sales, the interpolated values should be accepted by the courts.

As well depth formulae are useful models illustrating the front/rear land relationships in ribbon retail development. The diagram attached illustrates the first principle of the concept; that the front land is more valuable than the rear land.

FRONT VERSUS REAR LAND



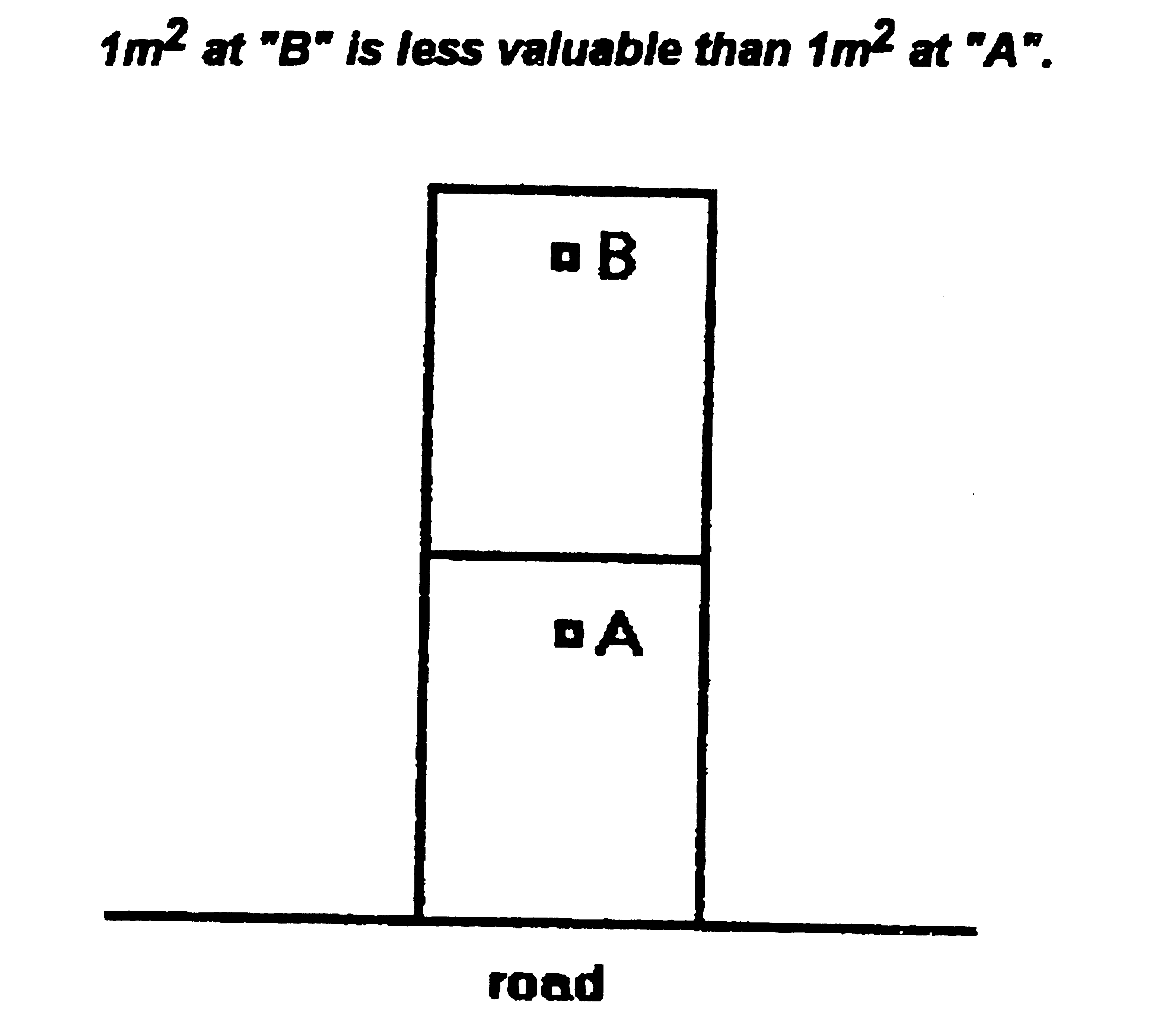
Depth formulae measure how much more valuable "A" is compared to "B". If lots 1 and 2 are situated in a ribbon development shopping centre, lot 2 is not twice as valuable as lot 1. Depth formulae can be used to determine how much more valuable lot 2 is compared to lot 1.

COMMON OR STANDARD DEPTH FORMULAE

A number of depth tables have been constructed from sale evidence in large cities in the western world. Although the valuer can construct his/her own formula (for example, with linear regression) from comparable sales, the relationship is not linear. Instead, the valuer may find a good fit from the existing curves. The goodness of fit can be tested using correlation coefficients. The best known depth formulae are:

All depth formulae assume the following:

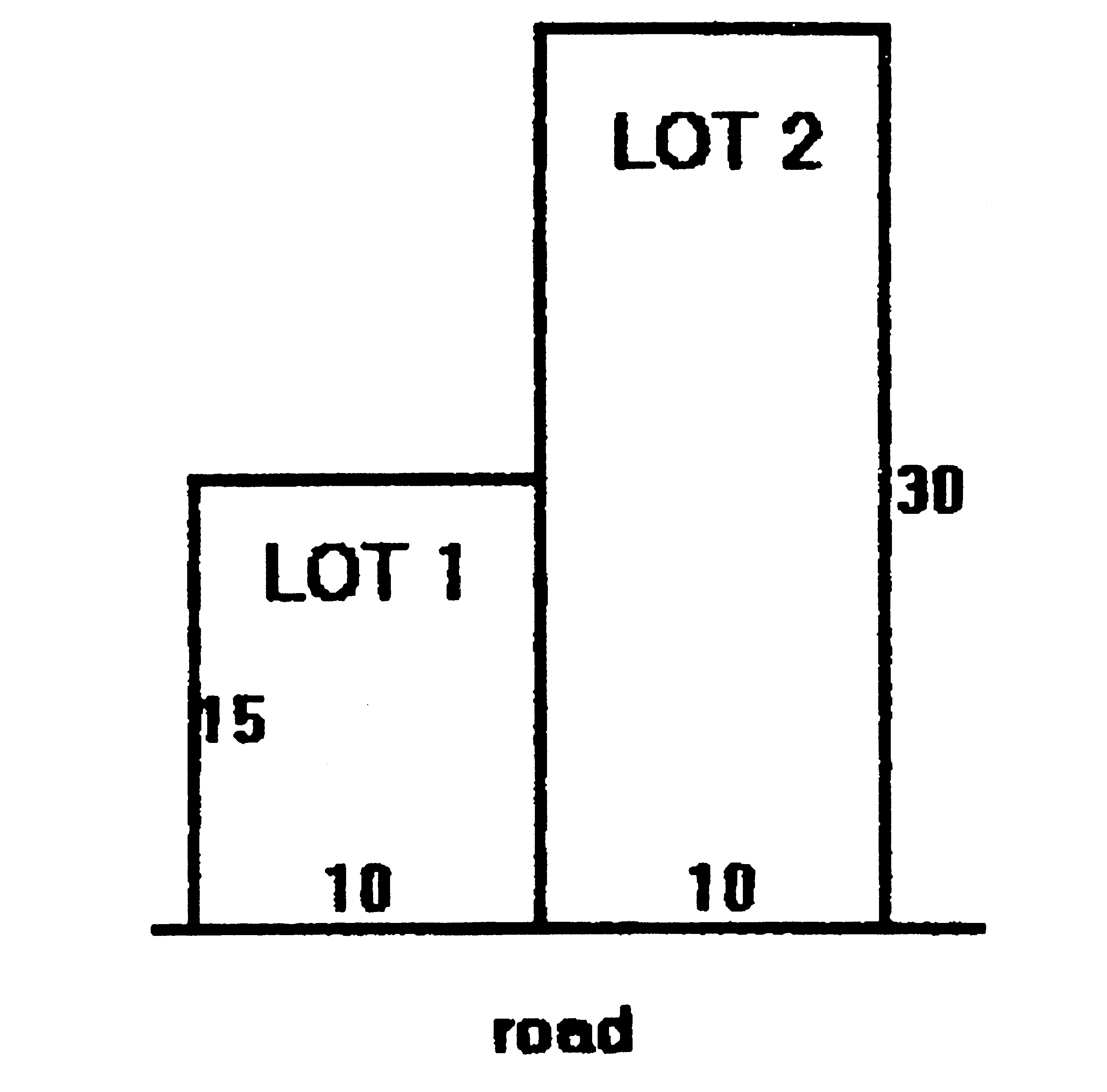
In the diagram below lot 2 has a value of 100% while lot 1 has a value less than 100%. It can be seen that the value of lot 1 is more than 50% of lot 2 because the front land is worth more than the rear land.


LOT 1 VERSUS LOT 2



THE HARPER RULE

Harper's  rule can be easily calculatdd for any block depth and any standard depth. All formulae calculate the depth factor (DF) that is the ratio of the value of the square lot to the value (ïf a lot with standard depth (expressed as a %). The Harper formula is:


DF = √d/√sd * 100

Where:

DF = depth factor as a %

d = depth in metres

sd = standard depth in metres.


EXAMPLE


Determine the depth factors for 3 lots with the following dimensions using the Harper Rule:

ANSWERS

Lot 1 = √20/√30 * 100 = 81.65%

Lot 2 = √28/√30 * 100 = 96.61%

Lot 3 = √10/√30 * 100 = 57.74%


The most common standard depth is 30m. The √30 = 5.477


STANDARD DEPTHS OTHER THAN 30 METRES


Non standard depths are easily calculated with Harper.

The depth factors for the above 3 lots with a standard depth of 40m are:


Lot 1 = √20/√40 * 100 = 70.71%

Lot 2 = √28/√40 * 100 = 83.67%

Lot 3 = √10/√40 * 100 = 50.00%

nb: √40 = 6.325 and √45 = 6.708.


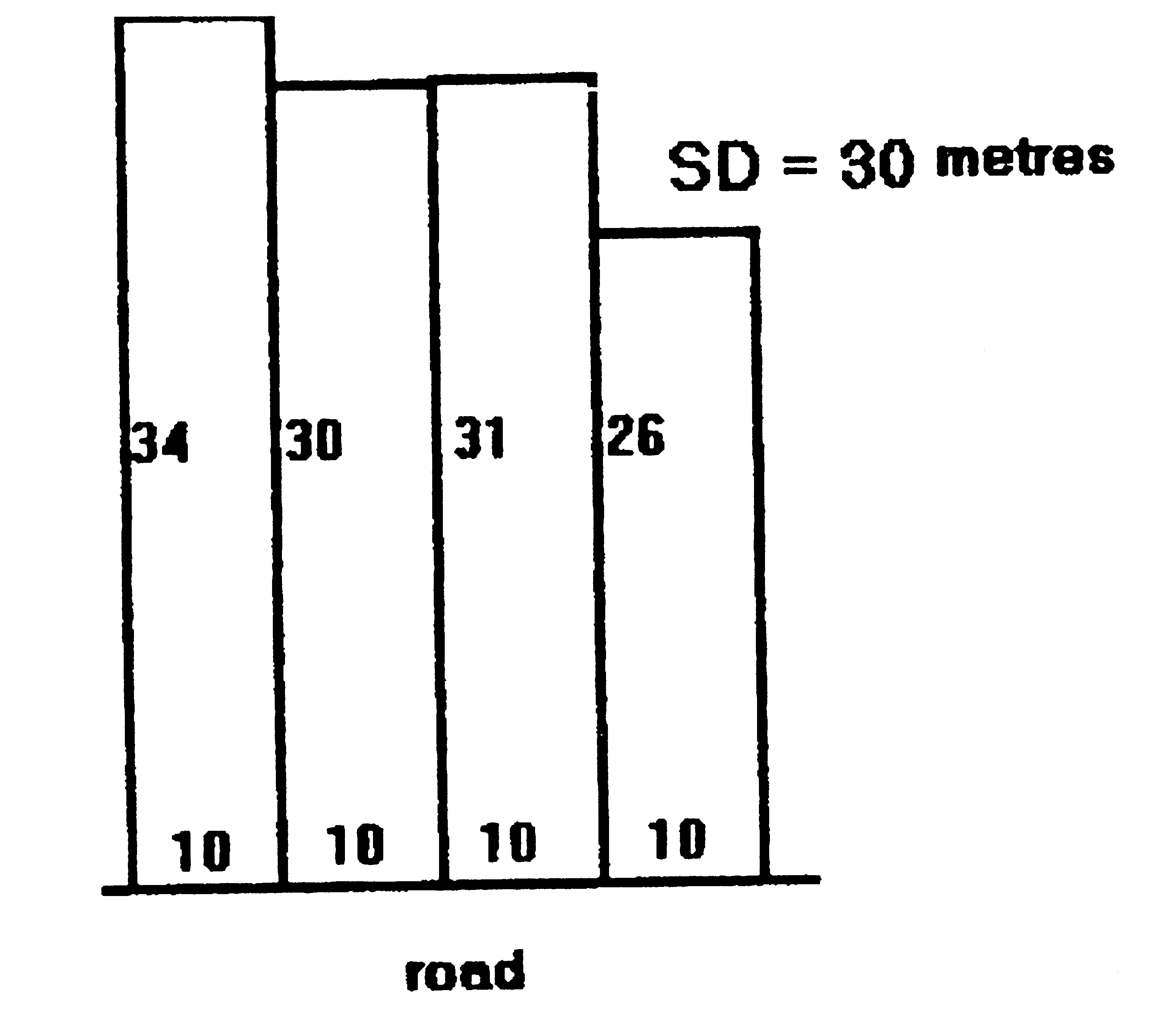
The chosen standard depth should be as near as possible to the depths of the majority of lots in the subject area. For example, the best standard depth for the shopping centre in the attached example is 30 metres:


30m SHOPPING CENTRE



THE AUSTRALIAN OR "4 3 2 1" RULE


The Australian rule subdivides a standard depth lot into 4*7.5 metre segments.

The rule states that each successive segment has a value in the ratio of 4:3:2:1 to the total block value. Therefore, the first 15m will represent 70% of the total value. Other depths can be interpolated from a graph of the curve.


4-3-2-1 RULE


THE "9 8 7 6" RULE

An extra 30m to the 4-3-2-1 rules is covered by the 9 8 7 6 rule. This states that the extra 4 * 7.5 metre segments beyond the standard depth of 30 metres attract an extra value of 9%, 8%, 7% and 6% respectively.

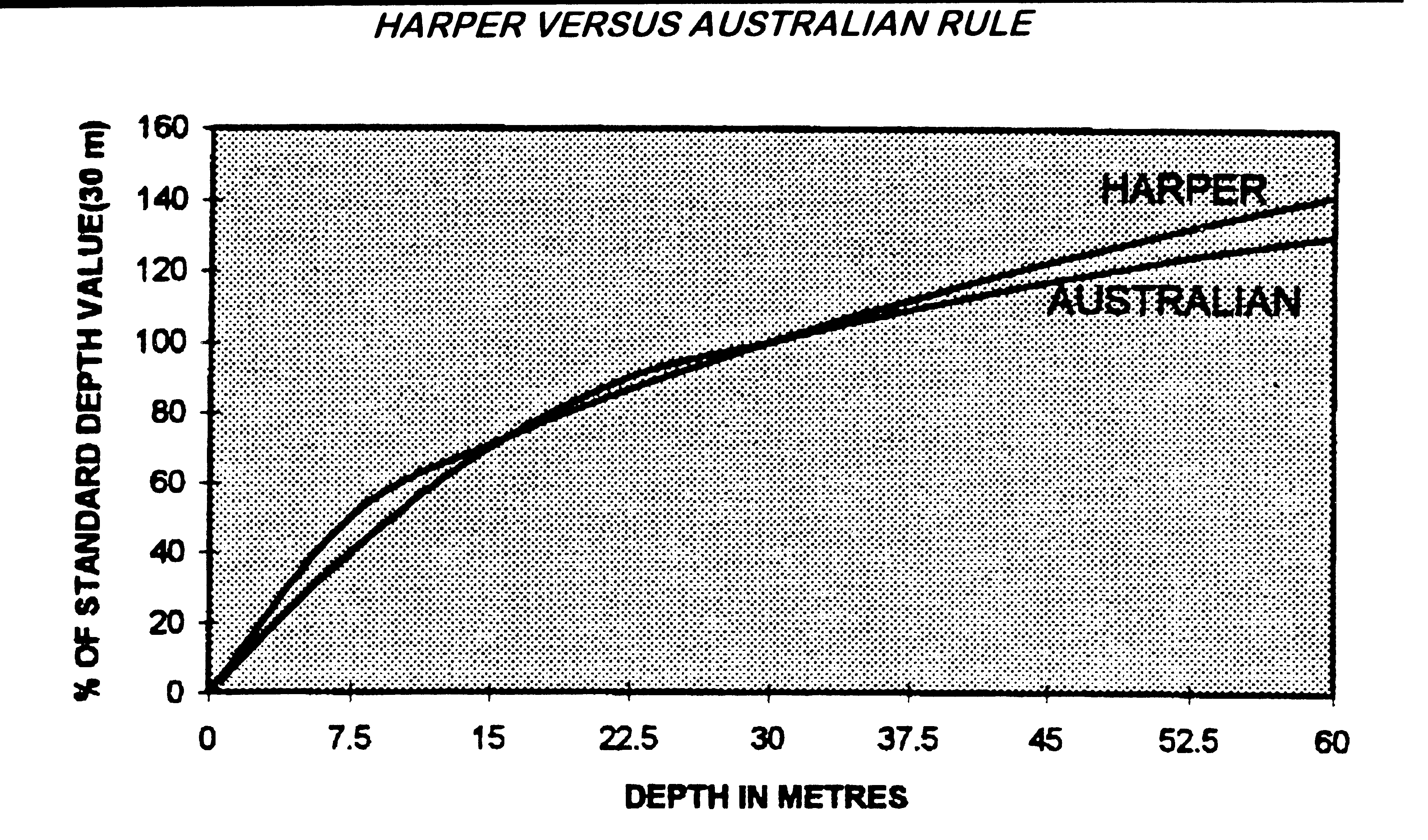
The Australian rule is constructed for a standard depth of 30 metres. It can be converted to other depths but not as easily as Harper. Therefore, it is recommended that Harper be used for non standard depths.


HARPER VERSUS AUSTRALIAN RULE



UNIT METRE VALUE (UMV)

Commercial ribbon development can be valued using depth formulae and unit metre value (UMV). Unit metre value is the value of a strip of land 1 metre wide at the standard depth.

The UMV is derived from sale evidence and is the common datum for comparison of ribbon development land values.


EXAMPLE

Determine the UMV for the commercial ribbon development lot in attached diagram if it has recently sold for $1 000 000.


BLOCK 10m WIDE


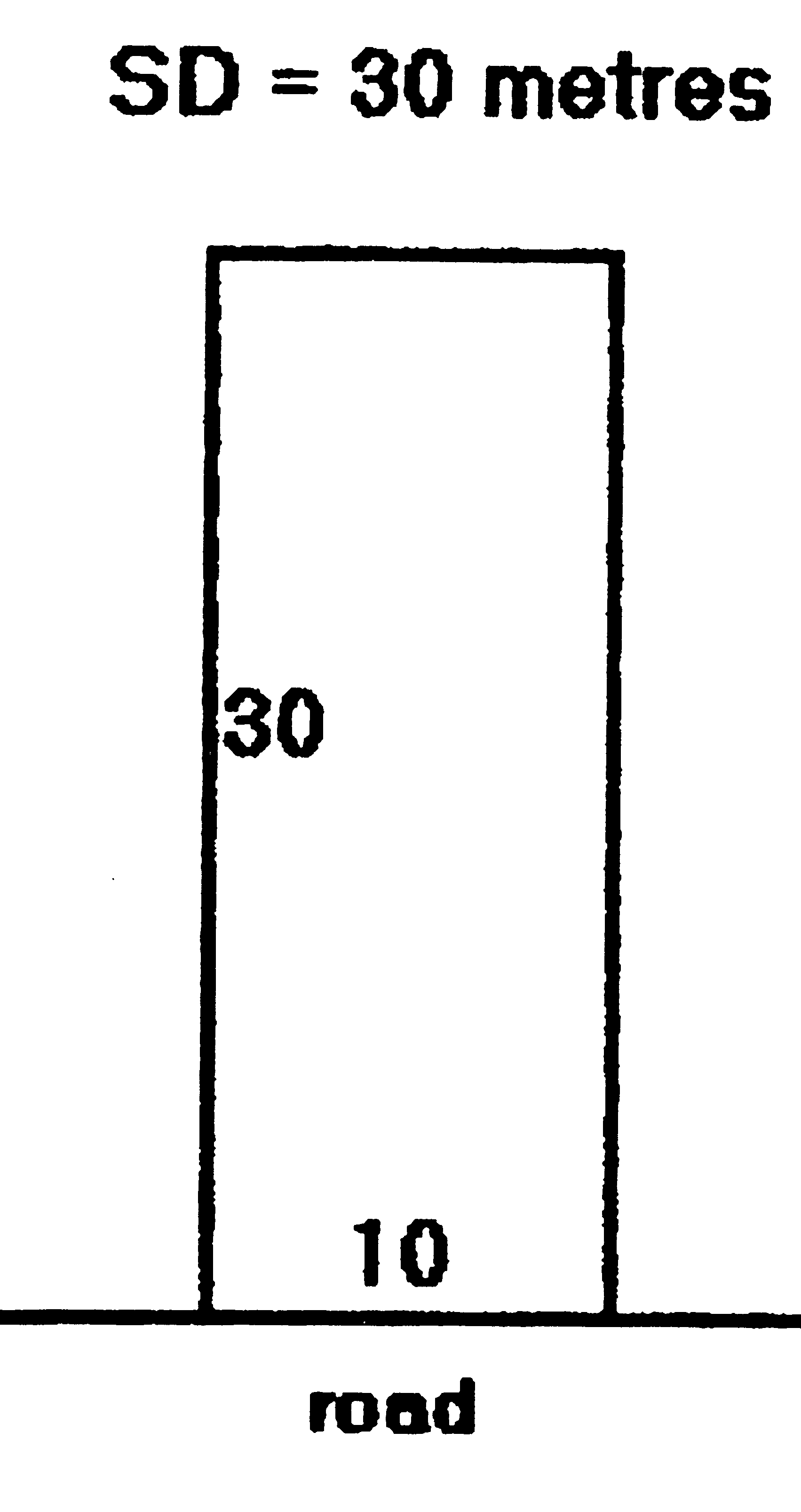
ANSWER:

UMV = 1000 000/10 = $100 000

EXAMPLE

Determine the value of the comparable lot that is 15m wide.

ANSWER:

Market value = 15 * 100 000 = $1 500 000


See depth table questions

See irregular blocks

9